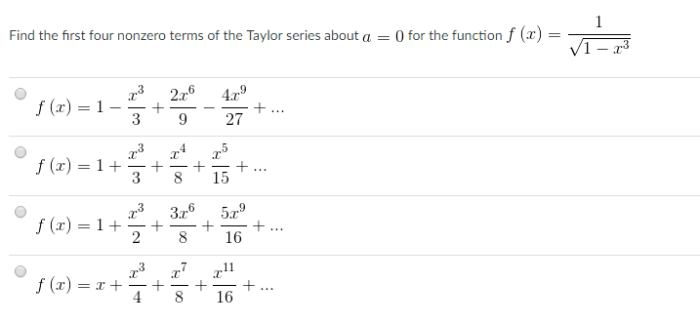Find the first four nonzero terms of the Taylor series is a fundamental concept in mathematics that provides a powerful tool for approximating functions. This guide will delve into the intricacies of Taylor series, explaining the process of finding the first four nonzero terms and exploring its applications in various fields.
Taylor series is a versatile mathematical tool that allows us to represent complex functions as a sum of simpler terms. By understanding the process of finding the first four nonzero terms, we gain insights into the behavior of functions and their derivatives.
Taylor Series

A Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function’s derivatives at a single point.
Mathematically, the Taylor series of a function \(f(x)\) about a point \(a\) is given by:
$$f(x) = f(a) + f'(a)(x-a) + \fracf”(a)2!(x-a)^2 + \fracf”'(a)3!(x-a)^3 + \cdots$$
Identify the First Four Nonzero Terms
To find the first four nonzero terms of the Taylor series for a function \(f(x)\) about a point \(a\), we need to calculate the values of the function and its first three derivatives at \(a\).
The first four terms are:
- \(f(a)\)
- \(f'(a)(x-a)\)
- \(\fracf”(a)2!(x-a)^2\)
- \(\fracf”'(a)3!(x-a)^3\)
Examples and Applications
Example 1: The Taylor series of \(f(x) = e^x\) about \(a=0\) is:
$$e^x = 1 + x + \fracx^22! + \fracx^33! + \cdots$$
Application 1: Taylor series are used in numerical analysis to approximate the values of functions.
Application 2: Taylor series are also used in physics to solve differential equations.
Error Estimation and Convergence, Find the first four nonzero terms of the taylor series
The error in truncating a Taylor series after \(n\) terms is given by:
$$R_n(x) = f(x)
P_n(x) = \fracf^(n+1)(c)(n+1)!(x-a)^n+1$$
where \(P_n(x)\) is the \(n\)th-degree Taylor polynomial and \(c\) is some point between \(a\) and \(x\).
A Taylor series converges if the limit of the error as \(n\to\infty\) is zero.
Advanced Topics
Advanced topics in Taylor series include:
- Remainder terms
- Applications in numerical analysis
Current research in Taylor series focuses on developing new methods for estimating the error and improving the convergence of Taylor series.
General Inquiries: Find The First Four Nonzero Terms Of The Taylor Series
What is the Taylor series?
The Taylor series is an infinite sum of terms that represents a function as a polynomial. It is a powerful tool for approximating functions and understanding their behavior.
How do I find the first four nonzero terms of the Taylor series?
To find the first four nonzero terms, you need to evaluate the function and its derivatives at a specific point. The formula for each term involves the derivative of the function and a power of the independent variable.
What are the applications of the Taylor series?
The Taylor series has applications in various fields, including physics, engineering, and computer science. It is used for approximating functions, solving differential equations, and modeling complex systems.